Megan Langford

During this activity, we will explore the behavior of pedal triangles. The first thing we need to do is to form the construction for our problem.

We will first label a triangle ABC. Then we will construct a point P and the perpendiculars to each side of the triangle. The intersection points of these lines will be labeled R, S, and T, and we will connect these points to construct our pedal triangle for pedal point P.

Our first example shows the pedal triangle when P is located outside the original triangle.

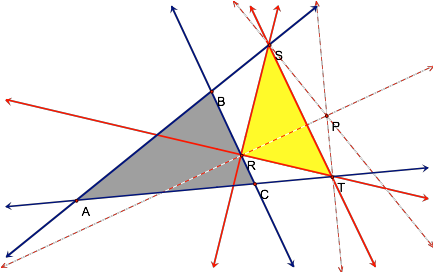
Here, the yellow shaded triangle is the pedal triangle for our original gray triangle and the pedal point labeled P.

In this case, our pedal triangle lies outside our original triangle and intersects the triangle on the side closest to the point P.

Let’s take a look at some pedal triangles where P is in different positions. First, let’s examine the case when P is inside the original triangle.

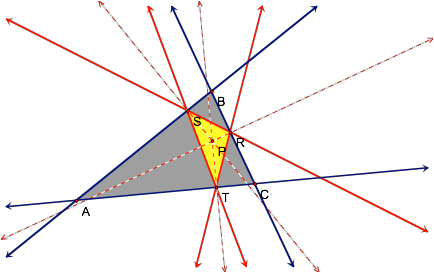
As we can see in the image above, it appears that when the pedal point P lies inside the original triangle, then the pedal triangle as well is contained within the original triangle.

To verify that this is in fact the case, let’s take a look at several more examples of P inside and outside of ABC.

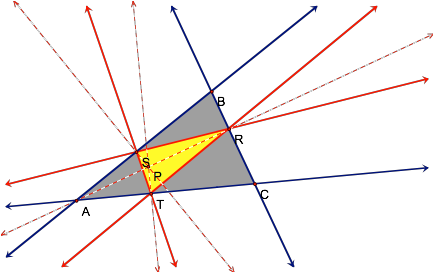
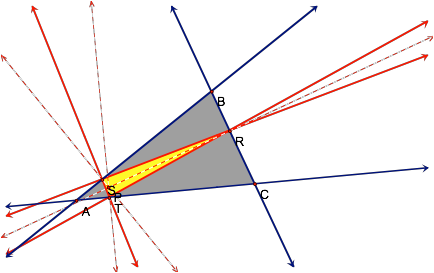
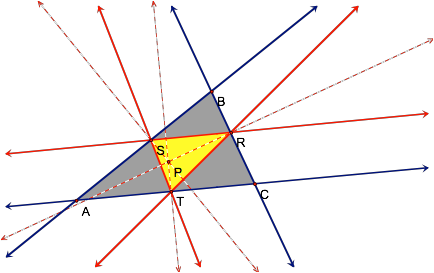
It does appear that every time P lies inside ABC, the pedal triangle is also contained within the gray triangle.

Now, let’s examine just a few more examples when P lies outside ABC.

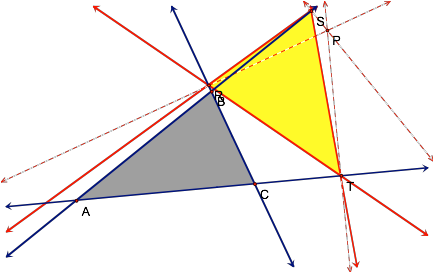
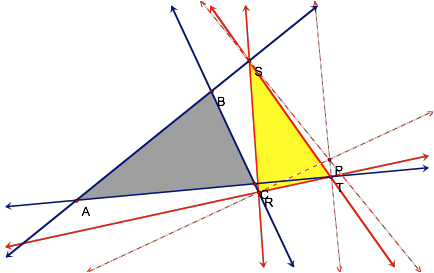
Yes, it does appear that our hypothesis has remained to be true. So at what point would we expect the pedal triangle to be when its position causes the pedal triangle to move from the inside of ABC to the outside? Let’s take a look at the pedal triangle when P lies on a side of the triangle.

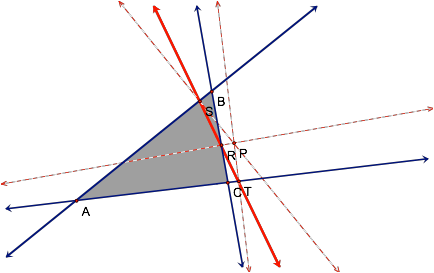
As we can tell from the image above, actually it turns out that the pedal triangle’s position moves from inside to outside the triangle ABC when the point P is just outside the original triangle (at least for a triangle of this shape). In fact, at this position, the pedal triangle has actually collapsed, since the three intersection points now fall along the same line. So what could be the significance of this point? Let’s explore this further by constructing the circumcircle around triangle ABC as we did in a previous exploration. Does this shed any light on the significance of P’s position?

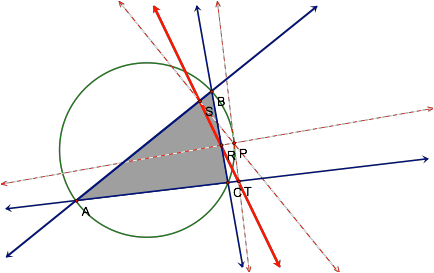
As it turns out, the pedal point here is lying directly on ABC’s circumcircle. Could this be a coincidence, or can we see more examples of this behavior?

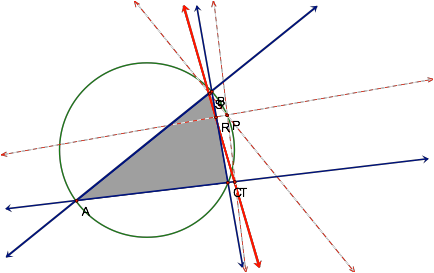
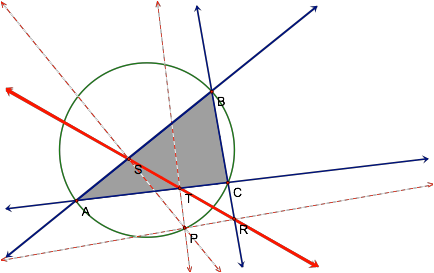
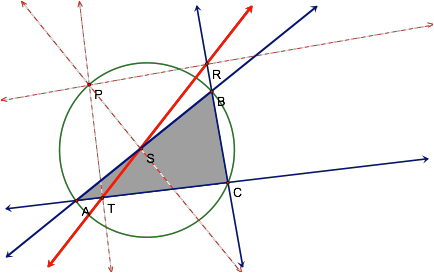
So, we can now adjust our hypothesis to conclude that the pedal triangle changes from being inside the original triangle to outside the original triangle as it collapses into a line whenever the pedal point P is located along the circumcircle.

After researching this behavior, we can learn that the line that is formed when the pedal triangle collapses is actually called the Simson Line.